CoBBl: a block-based approach to SNARK

What is Verifiable Computation and SNARK?

Imagine yourself as a user of cloud computing. You want to outsource a computation to a remote server, but the server might be unreliable or even malicious, so you wonder: how can I be convinced that the output I receive is correct? This problem of verifiable computation was first formulated in the early 90s, but is becoming increasingly popular recently with the rise of crypto currencies, where, every few minutes, the integrity behind millions of transactions falls onto the shoulder of a single anonymous entity. Verifiable computation has since inspired hundreds of research projects across the globe, motivates an entire DARPA program, and becomes the backbone of a billion-dollar industry.

How to make computations verifiable? One popular approach is through Succinct Non-Interactive Argument of Knowledge (SNARK). In this setup, as the remote machine executes the program, it produces a SNARK proof, which can be used to convince the user of the correctness of the output in time sublinear to the computation. We call the untrusted server that generates the proof the Prover ($\mathcal{P}$) and the user who verifies the proof the Verifier ($\mathcal{V}$).

A SNARK protocol usually contains three steps:

1. Compilation: $\mathcal{V}$, either on its own or through a trusted third party, converts the computation $\Psi$ into some form of a constraint system $\mathcal{C}$, the satisfying assigment of which can only be obtained if $\mathcal{P}$ correctly executes the program. This compilation phase only needs to be performed once per program (and, in some variants, once for all programs), and is often referred to as the frontend of a SNARK system.
2. Proving: given an input $x$, $\mathcal{P}$ executes $\Psi(x)$ to produce an output $y$ and additional witnesses $w$. It then proves that $(x, y, w)$ satisfies $\mathcal{C}$ in a SNARK proof $\pi$ using one of the many backend proof protocols (examples include GKR or Spartan).
3. Verifying: $\mathcal{V}$ checks the validity of $\pi$. If $\mathcal{P}$ behaved, it always accepts $y$; otherwise, it rejects with overwhelming probability.

A variant of SNARK called zkSNARK also emphasizes on an additional zero-knowledge property, where the verifier does not learn anything about the witnesses $w$. This is out of scope for this blog post, but note that the prover can convert a SNARK into a zkSNARK by producing an additional zero-knowledge proof on the correctness of the original proof.

It’s about the execution model!

Regardless of which exact constraint system $\mathcal{V}$ chooses, or what backend proof protocol $\mathcal{P}$ and $\mathcal{V}$ agree on, performance is always a big concern: the prover needs to run fast enough to minimize gas fees; the proof size needs to be small enough to fit into a blockchain; and the verifier cost needs to be efficient for even the cheapest mobile hardware. While SNARK researchers never fail to deliver on better cryptographic concepts, backend system design, and even brand new constraint representation, they often overlook an equally important aspect — the execution model of the proof system.

Conceptually, an execution model is the interface between a program’s semantics and its execution substrate. A fitting execution model enables the proof system to efficiently represent the computation, while incongruities lead to “wastes” — excessive descriptions that could otherwise be unnecessary. Currently, almost all existing SNARK systems adopt one of the two predominant execution models : direct translators and CPU emulators (also commonly referred to as zkVMs, even though many of the zkVM systems are not zero-knowledge).

The most notable direct translators include Pequin and CirC. These SNARK systems contain a built-in compiler that translates a program in a high-level language into one monolithic set of constraints $\mathcal{C}$. A compiler of a direct translator has full access to program structures and semantics, which enables it to capture program constructs that are efficiently expressable in constraints. They can also apply clever optimizations to take advantage of the nondeterministic nature of the constraints, achieving massive savings. The downside, however, is that the constraints $\mathcal{C}$ need to be fixed at compile time, so it must account for all execution paths of $\Psi$. In practice, the compiler needs to flatten the control flow of $\Psi$: encode both branches of every if / else statement, inline all function calls, and unroll every loop up to a static depth. Thus, $\mathcal{P}$ and $\mathcal{V}$ always pay the cost of both if and else branches, and the maximum costs for all loops regardless of the actual number of iterations.

Direct translators have the exact execution model as the constraint formalism $\mathcal{C}$, which enables them to produce optimized constraints for a given program. However, they fail to take advantage of other features of the proof system: namely, its design for highly data-parallel computations and the availability of specialized proof constructs, such as memory coherence check and lookup arguments, which are often performed more efficiently out-of-circuit than within $\mathcal{C}$. This flaw, combined with the static nature of the monolithic constraints, makes direct translators less appealing to modern crypto industry.

CPU emulators like vRAM and Jolt take on a completely different approach: instead translating the computation $\Psi$ directly to constraints, they use a set of pre-generated constraints to prove that $y$ is the output of a CPU that applies a correct sequence of fetch-decode-execute cycles to compute $\Psi$. To build a CPU emulator, a trusted programmer first determines an instruction set: most popular option includes TinyRAM, EVM, and RISC-V. Next, they generate the constraints for the correctness of each instruction. Finally, for a given program $\Psi$, the verifier $\mathcal{V}$ uses an off-the-shelf compiler to convert $\Psi$ into a list of instructions. The prover $\mathcal{P}$ proves the correct execution of each instruction through their corrsponding constraints, as well as the integrity of the CPU model itself: register state, instruction fetching, memory coherence, etc.

CPU emulators allow $\mathcal{P}$ and $\mathcal{V}$ to only pay for what it executes (i.e. no control-flow flattening). However, by keeping a fixed set of constraints independent of $\Psi$, CPU emulators lose opportunities to program-specific, constraint-level optimizations. Furthermore, the execution model of a CPU often misaligns with that of a proof system. Most notably, a regular CPU routine introduces a call stack to work around limited register space and leverage the memory hierarchy; in a proof system, however, registers are effectively unlimited while all memory accesses are equally expensive. Emulating a call stack — as most CPU emulators do — introduces unnecessary memory accesses and leads to inefficiencies in the proof.

The best of both worlds

Facing the two execution models with starkly different merits and drawbacks, we raise the natural question: can we create a new SNARK system that emits constraints tailored for individual programs, avoids excessive memory accesses, and allows the prover to only pay for what it executes? The key to our innovation lies in an execution model designed for the proof system, which should fully leverage data-parallelism within the computation, yet minimize data transfer between these data-parallel segments. We base our execution model on the concept of basic blocks, and name our SNARK system CoBBl (Constraints over Basic Blocks).

In essence, a basic block is a straight-line sequence of instructions with no internal branches; once $\mathcal{P}$ starts executing it, all instructions are executed sequentially unless an exception intervenes. Consequently, by basing the proof on a sequence of executed basic blocks, $\mathcal{P}$ and $\mathcal{V}$ never pay for instructions it does not execute. To build an efficient block-based SNARK system, however, there are a few lingering obstacles:

1. Designing a sound and efficient interface between basic blocks. Not only does $\mathcal{P}$ rely on the interface to switch between blocks during execution, the integrity proof of such interface is also essential for overall correctness. Unlike CPU emulators which strictly adhere to a CPU abstraction (or direct translators which do not have state passing), CoBBl’s block-based system supports program-specific transition state between blocks.
2. Maximizing block size and minimizing the number of unique blocks. Programs that are sufficiently complex are often representable with constraints simpler than those derived instruction by instruction. To leverage this property, CoBBl must also emit program segments that are adequately large. Furthermore, since the proof is based on basic blocks, the costs for $\mathcal{P}$ and $\mathcal{V}$ inevitably scale with the number of unique blocks. These two factors together necessitate a mechanism in CoBBl for merging smaller blocks.
3. Implementing an end-to-end compiler. To express arbitrary programs in its block-based execution model, CoBBl relies on a full compiler pipeline: dividing a program into basic blocks, merging and performing optimizations on each block, encoding all blocks as constraints, and presenting them in a way for a backend proof system to generate a SNARK proof.

Our foundation: a data-parallel backend proof system

CoBBl’s goal is to support most existing backend proof protocols with limited modification. Thus, we elide details on CoBBl’s concrete implementation and instead present a general framework of backend protocols that CoBBl operates on. In particular, we list three fundamental aspects of a CoBBl-compatible backend:

1. Data-parallelism: $\mathcal{P}$ proves the satisfiability of multiple assignments to the same constraint set (i.e. the same block) in linear time, while $\mathcal{V}$ verifies in sublinear time. Thus, $\mathcal{V}$’s cost is linear only in the number of unique blocks; all other factors are sublinear. Since the number of unique blocks is asymptotically smaller than the overall execution size, CoBBl’s proof remains succinct.
2. Offline memory check: $\mathcal{P}$ proves memory coherence across the entire execution in time linear to number of memory accesses. $\mathcal{V}$ verifies in time sublinear to number of memory accesses.
3. Cross-constraint lookup: given a claim on a pair of assignments drawn from two (possibly distinct) constraint sets, $\mathcal{P}$ can establish the claim over multiple assignment pairs in time linear in the number of pairs, while $\mathcal{V}$ verifies in time sublinear in the number of pairs. This primitive enables $\mathcal{P}$ to efficiently demonstrate the correctness of transitions between different block types.

The CoBBl frontend

Finally, we present our new block-based SNARK system. Building a SNARK system is hard, but fortunately we do not have to do it from scratch. Our starting point is CirC, a direct translator that can process, among other languages, a custom language called Z# specifically designed for SNARKs. CirC parses a Z# program into a syntax tree, turns the syntax tree into constraints, and expresses the constraints into formats compatible for various backend systems. The main modification of CoBBl is at the syntax tree layer. Specifically, CoBBl divides the program into blocks based on the syntax tree. It then performs optimizations on, and across blocks. Finally, it converts each block to constraints using existing functionalities of CirC. Below, we show a simple example of CoBBl in action, converting a find_min program into constraints through three stages.

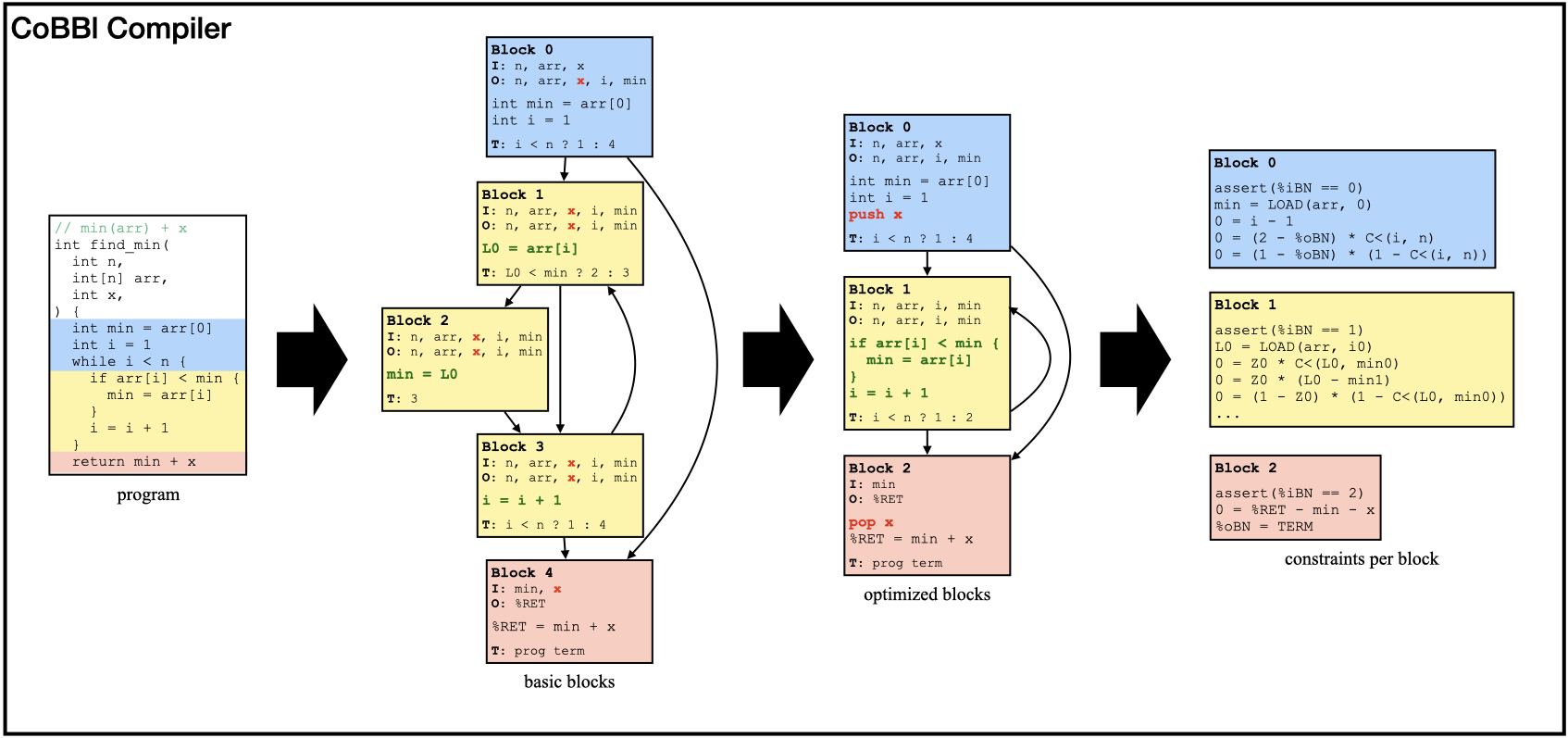
Divide a program into basic blocks

Each basic block is consisted of three components: a header that contains the block label, inputs, and outputs; a sequence of instructions executed by the block; and a transition statement that either specifies the transition to the next block, or marks program termination. At the end of the execution, the program output is stored in a special register, %RET.

Since basic blocks does not contain control flow, CoBBl generates them by linearly scanning the program, and initializing a new block every time the program control flow graph splits or merges (e.g. a start or an end to a branching statement or a loop). To ensure that no duplicate blocks are generated for a function with multiple callsites, CoBBl introduces another special register %RP to record the label of the return block after a function call. Every callsite to a function sets their own %RP, and every function terminates by returning to the block labeled by %RP.

After producing all the basic blocks, CoBBl also produces a round of “standard” compiler optimizations on each block, including liveness analysis, constant propagation, and inlining all functions with only one callsite (i.e., replacing %RP with its only possible value).

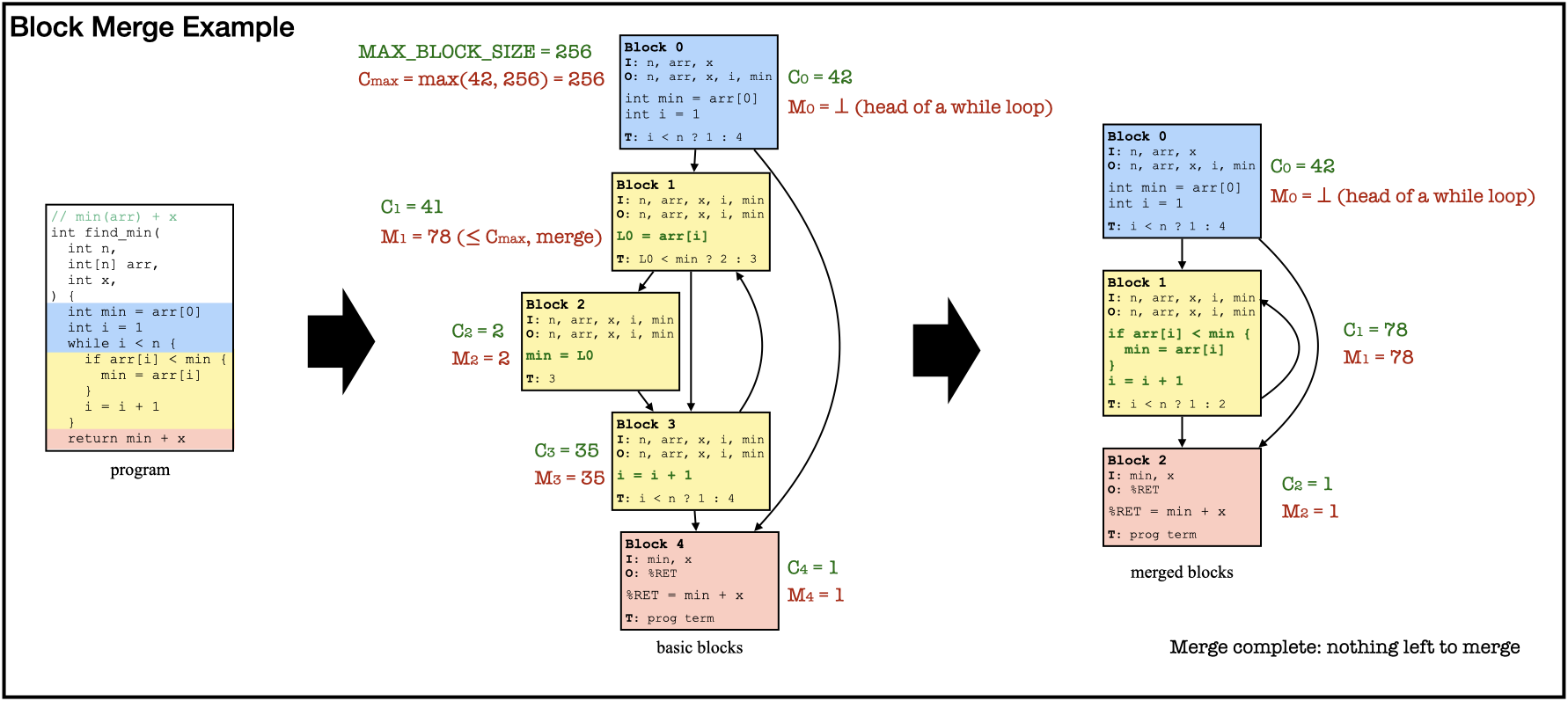
Minimize the number of blocks and optimize each block

Generating blocks solely off program control flow often lead to large quantity of small blocks. As explained earlier, this increases $\mathcal{V}$‘s cost and hinders CoBBl’s ability to find constraint-friendly representations. In the find_min example above, block 1, 2, and 3 each only have one instruction. Yet, for each execution of these blocks, $\mathcal{P}$ and $\mathcal{V}$ need to prove and verify the correct passing of the five input variables, and the block transition. This results in cost blowups. CoBBl addresses this by selectively merging smaller blocks into larger ones using existing flattening techniques (as in direct translators). The program is now expressable with fewer and larger blocks, but these blocks contain branches, and $\mathcal{P}$ and $\mathcal{V}$ now bear the cost of all execution paths. CoBBl captures this tradeoff in a user-defined parameter, MAX_BLOCK_SIZE, and the rest of the procedure is as follows:

1. CoBBl estimates the number of constraints $|\mathcal{C}_b|$ for each block $b$. It then deduces $|\mathcal{C}_{\text{max}}|$, the maximum size allowed for a merged block, computed as the maximum between MAX_BLOCK_SIZE and $\max_b|\mathcal{C}_b|$.
2. To merge blocks, CoBBl keeps track of $\mathcal{M}_b$, the estimated size of the merged block starting at block $b$. In particular:
   • If $b$ does not initiate a conditional jump, then CoBBl sets $\mathcal{M}_b$ to $|\mathcal{C}_b|$.
   • If $b$ initiates a function call, merging is undesirable — any uninlined function has multiple callsites. To denote this, CoBBl sets $\mathcal{M}_b = \bot$.
   • If $b$ is the head of a loop of unknown bound, CoBBl does not know how many times to unroll the loop, so it sets $\mathcal{M}_b = \bot$ and leaves the loop unchanged.
   • Finally, if $b$ is the head of a conditional jump with branch targets $\ell$ and $r$, and join point block $t$, CoBBl recursively computes $\mathcal{M}_\ell$, $\mathcal{M}_r$, and $\mathcal{M}_t$; merging all of these blocks together would yield a block of size $\mathcal{M}_b = |\mathcal{C}_b| + \mathcal{M}_\ell + \mathcal{M}_r + \mathcal{M}_t$.
     If $\mathcal{M}_b \leq |\mathcal{C}_{\text{max}}|$, CoBBl flattens $b, \ell, r, t$ into a single block; otherwise, it leaves them alone. Unrolling a loop of static bound $n$ is similar, except $\mathcal{M}_b = |\mathcal{C}_b| + n\cdot\mathcal{M}_{body} + \mathcal{M}_t$.
3. CoBBl repeats step 2 until either no more block can be merged, or every $\mathcal{M}_b$ exceeds $|\mathcal{C}_{\text{max}}|$.

Below, we demonstrate block merge in action on the find_min example:

Design an interface between blocks

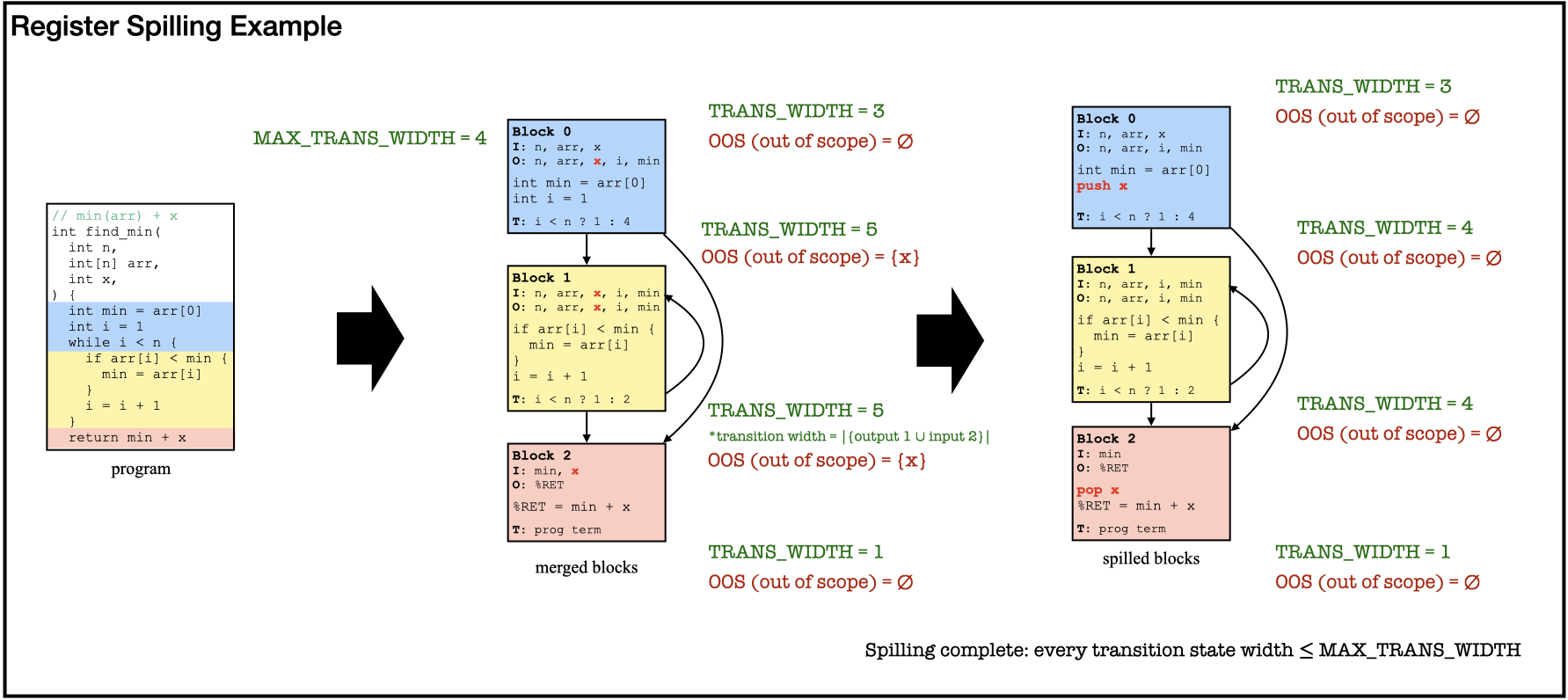
Even with the most constraint-friendly block format, the proof is incomplete without $\mathcal{P}$ establishing consistency of the program state across block transitions. Specifically, block transition needs to preserve the value of all non-local variable. CoBBl offers two mechanism to transmit the value of a variable $x$ from block $i$ to block $i+1$: as a register or through the scope stack.

CoBBl’s block design includes a set of input and output registers. During each transition from block $i$ to $i+1$, CoBBl uses cross-contraint lookup to establish that the output of block $i$ matches the input of block $i+1$. Thus, to pass $x$ as a register, CoBBl simply includes $x$ in the transition state.

The alternative is to spill $x$ onto the scope stack. This is particular useful when $x$ is out-of-scope across multiple blocks (say, block $i$ to $i+k$). In that case, including $x$ in all input and output states of block $i$ to $i+k$ introduces significant overhead. Instead, CoBBl pushes $i$ to the scope stack right before block $i$, and pops it back out right after block $i+k$. CoBBl’s scope stack is heavily inspired by the x86 call stack: it keeps track of a stack pointer %SP, and pushes and pops register values according to a static offset to %SP. Unlike x86, however, CoBBl initiates a new stack frame for every scope change (instead of function call), which allows CoBBl to spill variables base on scope. Below we demonstrate an example of register spilling:

Finishing touch and future work

After the two main optimizations and other standard compiler optimizations, CoBBl emits one constraint set for each optimized block, together with metadata such as the input size, output size, and number of memory accesses for each block type. The backend system uses this information to construct its own cross-constraint lookup and offline memory-check mechanisms. During execution, the prover supplies assignments to the block-level constraints (optionally via the CoBBl frontend) and to the auxiliary checks. The backend then aggregates these into a data-parallel proof over the entire execution, which the verifier checks in time sublinear to program execution.

By adopting a new block-based execution model, CoBBl becomes the first SNARK system to emit constraints tailored for individual programs, avoid excessive memory accesses, and allow the prover to only pay for what it executes. While the current implementation of CoBBl already outperforms several state-of-the-art direct translators and CPU emulators, CoBBl’s framework suggests even greater potential.

On the compiler side, CoBBl currently applies optimizations analogous to those in traditional compilers, where optimizations are constrained to respect execution dependencies. In a SNARK context, however, this requirement is unnecessary: an ideal compiler should instead exploit the nondeterministic nature of SNARKs. On the proof system side, CoBBl is well-positioned to incorporate recent advances such as lookup arguments and improved permutation checks. A tighter integration between compiler design and these proof techniques could enable circuits that dynamically introduce lookups, yielding significant efficiency gains.